無題Name名無し26/01/17(土)00:03:35No.124477そうだねx1
4月21日頃消えます[返信]
無題Name名無し26/01/17(土)00:03:35No.124477そうだねx1
4月21日頃消えます[返信]
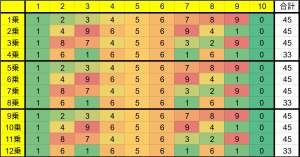
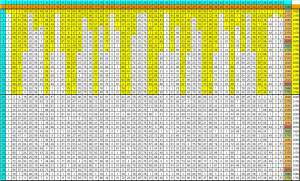
面白い事実ですねレス51件省略。全て読むには返信ボタンを押してください。
正答率が低いのも面白い
| … | 52無題Name名無し 26/02/15(日)12:04:34No.124658+>No.124655 |
| … | 53無題Nameベイズ厨 26/02/15(日)13:16:16No.124659+姉妹のパズルはボソンなら1/2 |
| … | 54無題Name名無し 26/02/15(日)13:36:20No.124660+>No.124659 |
| … | 55無題Nameベイズ厨 26/02/15(日)16:45:36No.124661+姉妹のパズルの話でボソンのとき |
| … | 56無題Nameベイズ厨 26/02/15(日)16:48:49No.124662+直感てシミュレーション両立するモデル |
| … | 57無題Name名無し 26/02/16(月)05:47:36No.124664+書き込みをした人によって削除されました |
| … | 58無題Nameベイズ厨 26/02/16(月)12:21:36No.124670+アナロジーとしてはどの点で気体分子を同一視するかという |
| … | 59無題Nameベイズ厨 26/02/16(月)12:51:46No.124671+シミュレーションに使ったランダムの定義と |
| … | 60無題Name名無し 26/02/17(火)08:29:00No.124677+すまんぬ訂正追加orz、 |
| … | 61無題Nameベイズ厨 26/02/18(水)06:05:36No.124680+配分の自由度が1回目の確率と2回目の確率の相関に影響 |