数学＠ふたば

画像ファイル名：1735903179363.jpg-(50948 B)

無題Name名無し25/01/03(金)20:19:39No.121464+ 12月14日頃消えます[返信]

良問オブザイヤー2024　大賞らしい

https://x.com/potetoichiro/status/1874985766960628104

…	1無題Name名無し 25/01/03(金)22:22:39No.121465+ 図形とかの問題だと、「あぁそこかー、そんなん思いつかねーよ」みたいなトンネルを抜けた開放感みたいなものがあるけど、こういう頓知か哲学か屁理屈かみたいな問いで答はこれです、言われても、便所の落書き以上の価値が見出せない。

画像ファイル名：1734527238575.png-(1114866 B)

無題Name名無し24/12/18(水)22:07:18No.121439+ 11月28日頃消えます[返信]

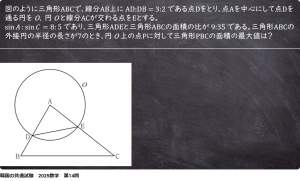
韓国の入試、キモすぎないか
何を計算させたいんだよ

…	1無題Name名無し 24/12/19(木)10:00:03No.121440そうだねx3 一息で出題されてるから分かりにくいけど問題を細分化して (1)BC:ABを求めよ (2)AB:ACを求めよ (3)∠Bを求めよ (4)AからBCに下ろした垂線の足をHとしたときAHを求めよ (5)△PBCの面積の最大値を求めよと考えれば一般的な数IA相当の問題

画像ファイル名：1731144247844.jpg-(307359 B)

無題Name名無し24/11/09(土)18:24:07No.121372+ 10月20日頃消えます[返信]

どのトマトも完全な球体で隙間なく入ってるとしたら、
一番量が多いのはどれ

レス19件省略。全て読むには返信ボタンを押してください。

…	20無題Name名無し 24/11/24(日)15:36:16No.121409+ 隙間にミニトマトを充填するとか？

…	21無題Name名無し 24/11/24(日)18:24:41No.121411+ >スレ画のように単位球を平面状に配置する場合は、1個の球に6個の球が接する形で >計7個の球が完全に接するので容器の寸法が無限大ならそれが最密 >有限の場合はより詰め込める非正規充填があるかもしれんが知らん四角い箱だと、７個より４個とか６個の方が詰まるかな。

…	22無題Name名無し 24/11/26(火)08:46:40No.121414+ 寸法2×2の箱に単位球を詰める場合は無限大のときと同じ配置にすると3個しか入らないが実際は4個入る 5個以上入れる方法が本当にないかわ知らん

…	23無題Name名無し 24/11/26(火)08:52:51No.121415+ んまー箱の面積が4で、単位球4個の箱の底への射影の面積が40.5^2πなので隙間の面積は4-40.5^2πとなってまだ単位球1個分より大きい面積が残っているからな (4-40.5^2π)-0.5^2*π=0.07300918301 > 0

…	24無題Name名無し 24/12/10(火)04:46:56No.121425+ スレッドを立てた人によって削除されましたさげ

…	25無題Name名無し 24/12/12(木)19:03:08No.121431+ スレッドを立てた人によって削除されましたさげ恥ずかしいやつがおるな

…

26無題Name名無し 24/12/14(土)22:08:35No.121434+

左様
トマトの大きさと箱の高さの関係を規定せずに出題するスレ主には出題センスが無い
トマト6個を3行2列でピッタリ入れられた画像があるから箱の縦横比は2:3で
高さは6個入り状態のトマト1個分と解釈するのは勝手やが
そうした瞬間スレ画の左と真ん中は題意から外れるから縦横比か高さのどれかには
解釈の余地があると解釈すべき……

縦横比2:3の箱に真円で密度ρのトマトを「底面に接する」形で詰めるとした場合、
個数6個をもって最大重量という回答のはそれはそうやが題意において箱の高さがフリーだとしたら
「底面に接する」を条件から外したらもっと詰まるし（ミニトマトを六方最密充填

で、縦横比2:3に解釈の余地があるとしたら、5個入りの方が重量のが大きい……
箱の大きさが2×3.2154なら
半径1のトマトだと6個入って重量は6ρπ*(3/4)*(0.5^3) = 0.5625 ρπ
半径1/(1+cosθ) (ただしsinθ=1/2)のトマトだと5個入って重量は5ρπ*(3/4)*((1/1+cosθ)^2)=0.5771ρπ

…	27無題Name名無し 24/12/16(月)21:31:02No.121435+ 現実にトマトの大きさが同じなわけないだろ

…

28無題Name名無し 24/12/17(火)07:42:42No.121436+

>現実にトマトの大きさが同じなわけないだろ

　　　　　　　　　　　　／）
　　　　　　　　　　　／／／）
　　　　　　　　　／,.=ﾞ''"／　　　
　　　／　　　　 i f　,.r='"-‐'つ　　こまけぇこたぁいいんだよ！！
　　/　　　　　 /　　　_,.-‐'~／⌒　　⌒＼
　　　　／　　,i　　　,二ﾆ⊃（ ●）.　（●）＼
　　　/　　　ﾉ　　　 ilﾞフ:::⌒（__人__）⌒:: ＼
　　　　　　,ｲ｢ﾄ､　　,!,!|　　　　|r┬-|　　　　|
　　　　　/　iﾄヾヽ_/ｨ"＼　　　 `ー'´ 　　／

…	29無題Name名無し 24/12/17(火)14:32:48No.121438+ >現実にトマトの大きさが同じなわけないだろエジソンも同じ考えで「１＋１＝２　なわけねーべ。プゲラ」とやって小学校退学なんだろうなあ

無題Name名無し24/12/03(火)19:27:19No.121417+ 11月13日頃消えます[返信]

https://www.youtube.com/shorts/jwrXmvKVV9E
なんでBDが2xなん？

…	1無題Name名無し 24/12/04(水)16:12:06No.121418そうだねx1 角の２等分線と比の定理ってのがあって、それを使う。

…	2無題Name名無し 24/12/05(木)00:03:08No.121419+ なる。

…	3無題Name名無し 24/12/07(土)17:35:54No.121422+ https://www.youtube.com/shorts/U9hOBZu0itc 等辺12cmのただの二等辺三角形の可能性は？

…	4無題Name名無し 24/12/07(土)21:02:11No.121423+ 問題の図からは直角の印が抜けているねｗ説明では直角二等辺三角形と言っているが

…	5無題Name名無し 24/12/14(土)18:43:57No.121433+ ただの二等辺三角形だとしたら・・・

無題Name名無し24/12/09(月)22:58:16No.121424そうだねx1 11月19日頃消えます[返信]

答えが合わなくて困っています。よろしくおねがいします。

例題　ある県の小学生全員を対象に消しゴムを何個持っているかを調査したところ，平均値(母平均)は10個，標準偏差(母標準偏差)は4個であることがわかった．この母集団から無作為に100人を選んだとき，この100人が持っている消しゴムの個数の平均
＿
X が12個以上である確率を求めよ．

…	1無題Name名無し 24/12/11(水)17:24:26No.121428そうだねx1 合ってるよ。ミスプリだから気にするな。

…	2無題Name名無し 24/12/11(水)22:13:24No.121429そうだねx1 ∫ from 12 to ∞ 1/√(2π*4^2) exp(- (x-10)^2/2/4^2) dx こいつを WolframAlpha で計算させると30.85%程度

画像ファイル名：1730884226427.jpg-(903792 B)

無題Name名無し24/11/06(水)18:10:26No.121365+ 10月17日頃消えます[返信]

数学の本

おなまえ
E-mail
題　　名
コメント
添付File	[画像なし]
削除キー	(記事の削除用。英数字で8文字以内)