 無題Name名無し25/08/10(日)12:05:55No.122031+
26年7月頃消えます[返信]
無題Name名無し25/08/10(日)12:05:55No.122031+
26年7月頃消えます[返信]
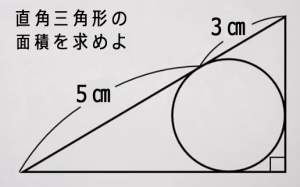
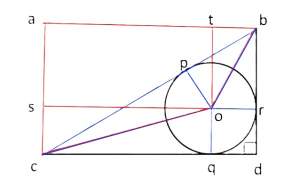
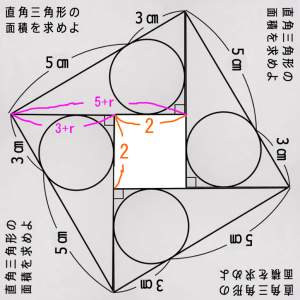
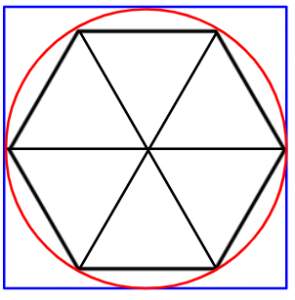
質問なのですが定規とコンパスで3等分できる角度は
360°とその2^(-n)倍の他に何か有り?
| … | 1無題Name名無し 25/08/10(日)12:09:36No.122032+あともう一個orz |
| … | 2無題Name名無し 25/08/10(日)13:18:11No.122033+60度の三等分の作図ってできんのでは? |
| … | 3無題Name名無し 25/08/10(日)15:51:41No.122034+3°の倍数の角は作図可能なので正整数の範囲で言えば9°の倍数の角は3等分可能 |
| … | 4無題Name名無し 25/08/10(日)20:09:00No.122036+ 1754824140039.png-(534725 B)  3°はどうやるのかわかり |
| … | 5無題Name名無し 25/08/11(月)03:51:07No.122037+角の三等分については40年以上前に日立市の人が… |
| … | 6無題Name名無し 25/08/11(月)09:22:50No.122039+>3°はどうやるのかわかり |
| … | 7無題Name名無し 25/08/14(木)16:40:54No.122050+そんなに重ねて重ねて描いてたら、コンパスの線の太さで誤差だらけになりそう・・・ |
| … | 8無題Name名無し 25/08/15(金)11:05:38No.122051+論理的に描けるのが保証できたらOK |
| … | 9無題Name名無し 25/08/15(金)22:18:29No.122053+ノーベル取った人だったか誰だったか・・・ |