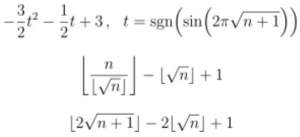画像ファイル名：1720358766042.png-(52447 B)
無題Name名無し24/07/07(日)22:26:06No.120924+ 15日03:25頃消えます[返信]

数列
1, 2, 3, 1, 1, 2, 2, 3, 1, 1, 1, 2, 2, 2, 3, 1, …
の一般項が画像のように書けるらしいんですが、どうやって求めたんでしょうか…
ちなみにOEISには載ってないです。

このスレは古いので、もうすぐ消えます。

…	1無題Name名無し 24/07/09(火)11:23:08No.120929+ ２行目と３行目はどうくっついているんだ？

…	2無題Name名無し 24/07/09(火)13:32:58No.120930+ >２行目と３行目はどうくっついているんだ？ 独立している 表す数列自体は同じだが1,2,3行目でそれぞれ別の表現 式の生成過程において2行目を元に3行目が導出された可能性はある