 無題Name名無し26/01/01(木)08:17:09No.124375+
4月04日頃消えます
無題Name名無し26/01/01(木)08:17:09No.124375+
4月04日頃消えます
2026年にちなんだ問題を作って出題してください削除された記事が6件あります.見る
例
2を6個と3を1つ使って2026をつくりなさい
1桁の数字としてだけでなく
2つ繋げて22とかにしてもOKです
他の計算記号も自由に使ってOKですが
2
2-2=0
√(2*2)=2
2×3=6
を並べて2026の様なのはなしでお願いします
| … | 1無題Name名無し 26/01/01(木)09:03:13No.124376そうだねx13×(22+2×2)^2-2=2026 |
| … | 2無題Name名無し 26/01/01(木)09:35:22No.124377+書き込みをした人によって削除されました |
| … | 3無題Name名無し 26/01/01(木)11:51:15No.124380+西暦問題の定番だけど |
| … | 4無題Nameベイズ厨 26/01/01(木)12:05:53No.124381+>124376 |
| … | 5無題Name名無し 26/01/01(木)12:50:04No.124382+>>124376 |
| … | 6無題Nameベイズ厨 26/01/01(木)13:00:56No.124383+なるほど |
| … | 7無題Name名無し 26/01/01(木)13:49:18No.124385そうだねx12025+1で作るなら(22+23)^2+2/2 |
| … | 8無題Name名無し 26/01/01(木)20:38:09No.124389そうだねx1 1767267489140.jpg-(2121651 B)  >西暦問題の定番だけど |
| … | 9無題Name名無し 26/01/01(木)20:39:21No.124390+>3×(22+2×2)^2-2=2026 |
| … | 10無題Name名無し 26/01/02(金)12:06:29No.124395+>3×(22+2×2)^2-2=2026 |
| … | 11無題Name名無し 26/01/02(金)12:35:46No.124397+>想定した答えと違いますが正解です |
| … | 12無題Name名無し 26/01/02(金)20:36:34No.124398+>>想定した答えと違いますが正解です |
| … | 13無題Name名無し 26/01/03(土)07:45:59No.124399+ 1767393959184.jpg-(119353 B)  問題1 |
| … | 14無題Name名無し 26/01/04(日)21:54:39No.124409+ 1767531279822.jpg-(19362 B)  x=3ではありません |
| … | 15無題Name名無し 26/01/04(日)22:44:25No.124410+>問題1 |
| … | 16無題Name名無し 26/01/05(月)01:03:06No.124411+>No.124399 |
| … | 17無題Name名無し 26/01/05(月)07:18:59No.124412+>>問題1 |
| … | 18無題Name名無し 26/01/05(月)17:37:28No.124420そうだねx1>1³+2³+3³+4³+5³+6³+7³+8³+9³=2025(去年話題になった等式)なので |
| … | 19無題Name名無し 26/01/05(月)18:43:06No.124421+>思い込みを捨て |
| … | 20無題Name名無し 26/01/06(火)00:46:51No.124423+ 1767628011228.png-(21572 B) 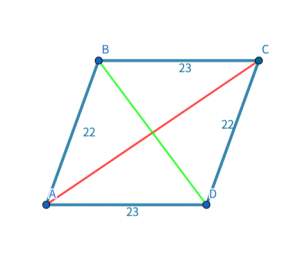 平行四辺形ABCDがある |
| … | 21無題Name名無し 26/01/07(水)00:19:42No.124431+>平行四辺形ABCDがある |
| … | 22無題Name名無し 26/01/07(水)08:06:51No.124432+>>思い込みを捨て |
| … | 23無題Name名無し 26/01/07(水)12:41:42No.124435そうだねx1 1767757302784.png-(78842 B) 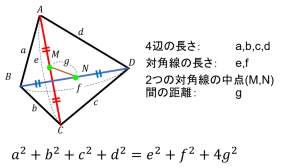 >No.124431 |
| … | 24無題Name名無し 26/01/07(水)12:43:33No.124436+>No.124435 |
| … | 25無題Name名無し 26/01/07(水)14:22:04No.124438そうだねx1 1767763324909.jpg-(125058 B) 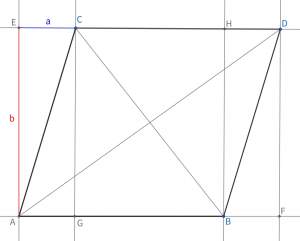 >→オイラーの四辺形定理 |
| … | 26無題Name名無し 26/01/07(水)18:59:31No.124439+>>22 |
| … | 27無題Name名無し 26/01/08(木)01:36:19No.124440そうだねx1>No.124438 |
| … | 28無題Name名無し 26/01/08(木)23:42:03No.124442+ 1767883323937.jpg-(61281 B) 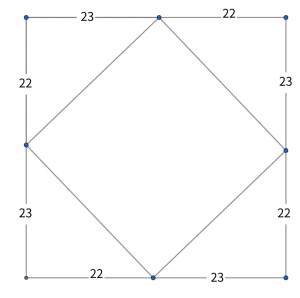 >さすがに小学生が図形的発想だけで導くのは難しいか…? |
| … | 29無題Name名無し 26/01/11(日)08:33:39No.124451+ 1768088019269.png-(2351863 B)  45m×45mの正方形のグランドの中に子どもが2026人います |
| … | 30無題Name名無し 26/01/11(日)17:39:45No.124453+統計学と思ったが、2026/81で25.01 |
| … | 31無題Name名無し 26/01/11(日)17:54:54No.124454+一般化された鳩ノ巣原理というやつだねえ |
| … | 32無題Name名無し 26/01/12(月)02:06:49No.124455+書き込みをした人によって削除されました |
| … | 33無題Name名無し 26/01/13(火)20:36:38No.124457+>統計学と思ったが、2026/81で25.01 |
| … | 34無題Name名無し 26/01/14(水)21:08:40No.124460+ 1768392520342.jpg-(42519 B)  画像の数列について問題です |
| … | 35無題Name名無し 26/01/14(水)23:22:54No.124461+>画像の数列について問題です |
| … | 36無題Name名無し 26/01/14(水)23:36:13No.124462+>類題 |
| … | 37無題Name名無し 26/01/15(木)11:56:45No.124465+類題 |
| … | 38無題Name名無し 26/01/15(木)22:25:54No.124467+>>画像の数列について問題です |
| … | 39無題Name名無し 26/01/15(木)22:51:20No.124468+ 1768485080903.jpg-(32581 B)  AB=22 |
| … | 40無題Name名無し 26/01/15(木)23:27:47No.124469+>面積が2026となる正方形を作図せよ(またはその方法を説明せよ) |
| … | 41無題Name名無し 26/01/16(金)21:57:55No.124473+ 1768568275889.jpg-(50298 B)  >(23+22)^2 + (23-22)^2 =2026 や |
| … | 42無題Name名無し 26/01/16(金)22:44:10No.124476+ 1768571050324.jpg-(69927 B)  >(22^2+23^2) + (22^2+23^2) =2026 を利用して |
| … | 43無題Name名無し 26/01/17(土)00:47:39No.124479+ 1768578459724.png-(71056 B)  >この直角三角形を利用して |
| … | 44無題Name名無し 26/01/17(土)07:35:01No.124483+ 1768602901344.jpg-(60186 B)  >アイディアは No.124476 と一緒だけど折角なのでコンパスの使用回数を1回のみに制限して作図してみた |
| … | 45無題Name名無し 26/01/18(日)20:46:23No.124505+周の長さが2026 |
| … | 46無題Name名無し 26/01/18(日)23:36:00No.124506+三辺の長さが自然数になる直角三角形が存在すると仮定する |
| … | 47無題Name名無し 26/01/19(月)19:59:09No.124509+>よって各辺の長さが自然数で周の長さが2026となる直角三角形は存在しない |
| … | 48無題Name名無し 26/01/22(木)21:00:40No.124520+問題です。 |
| … | 49無題Name名無し 26/01/22(木)23:00:56No.124521そうだねx1>問題です。 |
| … | 50無題Name名無し 26/01/23(金)20:19:00No.124525+ 1769167140254.jpg-(81258 B) 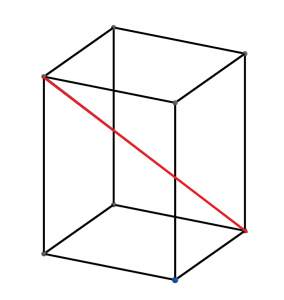 3辺の長さがそれぞれ自然数a,b,c(a>b>c)となるような直方体があります |
| … | 51無題Name名無し 26/01/24(土)01:56:59No.124526+>3辺の長さがそれぞれ自然数a,b,c(a>b>c)となるような直方体があります |
| … | 52無題Nameベイズ厨 26/01/24(土)07:59:19No.124527+>丙午 |
| … | 53無題Name名無し 26/01/24(土)19:49:12No.124530+ 1769251752983.jpg-(2714402 B)  >必ず(3の倍数,3の倍数,9で割ると1か8余る数)とかまでは分析したけど後はゴリ押しした |
| … | 54無題Name名無し 26/01/25(日)02:06:12No.124531+書き込みをした人によって削除されました |
| … | 55無題Name名無し 26/01/25(日)02:39:26No.124532+大きさの異なる2つの半球 A, B があります。 |
| … | 56無題Name名無し 26/01/25(日)07:25:56No.124534+>大きさの異なる2つの半球 A, B があります。 |
| … | 57無題Name名無し 26/01/25(日)09:59:44No.124537+ 1769302784811.jpg-(136256 B) 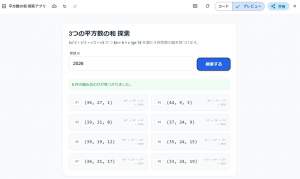 >>必ず(3の倍数,3の倍数,9で割ると1か8余る数)とかまでは分析したけど後はゴリ押しした |
| … | 58無題Name名無し 26/01/25(日)13:49:01No.124540+>No.124534 |
| … | 59無題Name名無し 26/01/25(日)13:53:29No.124541+便乗で恐縮なのですが |
| … | 60無題Name名無し 26/01/25(日)15:44:52No.124542+>No.124541 |
| … | 61無題Name名無し 26/01/25(日)17:09:41No.124543+ 1769328581606.jpg-(100330 B) 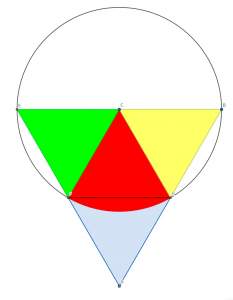 >>No.124541 |
| … | 62無題Name名無し 26/01/26(月)07:12:10No.124546+ 1769379130606.jpg-(24663 B) 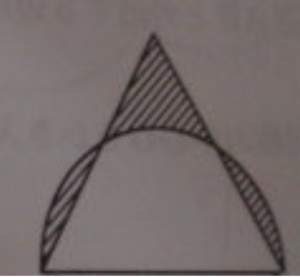 >底辺を共有する半円と正三角形の共有部分の面積の整数部分(小数点以下切り捨て)が2026となるのは半円の半径が○○.〇のときである |
| … | 63無題Name名無し 26/01/26(月)10:09:18No.124547+書き込みをした人によって削除されました |
| … | 64無題Name名無し 26/01/26(月)11:13:42No.124548+>No.124543 |
| … | 65無題Name名無し 26/01/26(月)18:50:19No.124550+ 1769421019165.jpg-(43030 B) 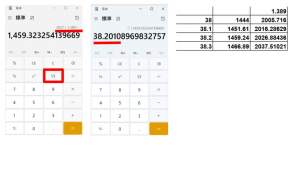 >となるため、r = 38.2 となる |
| … | 66無題Name名無し 26/01/27(火)06:57:59No.124553+初項から第n項までの和が2026になるおもしろい数列を考え |
| … | 67無題Name名無し 26/01/29(木)19:14:57No.124555+ 1769681697437.jpg-(55907 B)  >初項から第n項までの和が2026になるおもしろい数列を考え |
| … | 68無題Name名無し 26/01/30(金)03:13:20No.124556+和ではないですが… |
| … | 69無題Name名無し 26/01/30(金)13:49:19No.124557+>No.124555 |
| … | 70無題Name名無し 26/01/30(金)20:44:02No.124559+ 1769773442594.png-(901179 B) 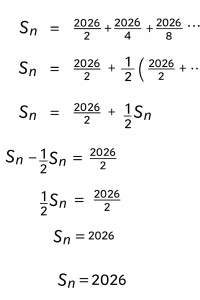 >No.124555 |
| … | 71無題Name名無し 26/01/31(土)14:38:23No.124563+ 1769837903668.jpg-(105888 B)  >和ではないですが… |
| … | 72無題Name名無し 26/02/01(日)20:32:26No.124566+ 1769945546130.jpg-(689773 B)  画像にある紙幣と硬貨を使った問題です。 |
| … | 73無題Name名無し 26/02/02(月)03:03:41No.124569+>問題1 a+b+c=31 |
| … | 74無題Name名無し 26/02/02(月)03:11:51No.124570+>>問題1 a+b+c=31 |
| … | 75無題Name名無し 26/02/02(月)06:52:54No.124571+>問題1 a+b+c=31 |
| … | 76無題Name名無し 26/02/02(月)06:53:48No.124572+○c=11の場合 → 紙幣A と 硬貨B の合計枚数20枚で 2015円を作る必要がある |
| … | 77無題Name名無し 26/02/02(月)11:37:10No.124574+書き込みをした人によって削除されました |
| … | 78無題Nameベイズ厨 26/02/02(月)11:43:55No.124575+あるんでしょうか、ないんでしょうか |
| … | 79無題Name名無し 26/02/02(月)18:57:12No.124580+>またはa+b+c=30の出題ミスか |
| … | 80無題Name名無し 26/02/03(火)05:10:01No.124588+いぼ痔患者みたいな奴いるな |
| … | 81無題Nameベイズ厨 26/02/03(火)05:31:57No.124589+グーグルやマイクロソフトの試験で |
| … | 82無題Nameベイズ厨 26/02/03(火)15:05:18No.124596+30のときの答えは? |
| … | 83無題Name名無し 26/02/03(火)20:22:05No.124600+>30のときの答えは? |
| … | 84無題Nameベイズ厨 26/02/04(水)07:43:34No.124601+ありがとうございます |
| … | 85無題Nameベイズ厨 26/02/04(水)11:49:51No.124603+(0 1) |
| … | 86無題Name名無し 26/02/06(金)22:44:05No.124610+ 1770385445429.png-(2685082 B)  先生が「天秤を使って1gから2026gまで1gきざみで測るには最低何個のおもりが必要か?」という問題をだしました |
| … | 87無題Name名無し 26/02/06(金)23:25:34No.124611+A:{2^(n-1)g}(1≦n≦11)の重りを用意する |
| … | 88無題Nameベイズ厨 26/02/07(土)09:13:46No.124612+観測対象の重さときざみ/おもり |
| … | 89無題Name名無し 26/02/08(日)00:01:07No.124622+>A:{2^(n-1)g}(1≦n≦11)の重りを用意する |
| … | 90無題Nameベイズ厨 26/02/08(日)06:06:11No.124623+124566の文脈から10進法と二進法の最小情報量表示なら1 |
| … | 91無題Nameベイズ厨 26/02/08(日)06:18:51No.124624+山本義隆先生の小数と対数の発見読みたいですが |
| … | 92無題Nameベイズ厨 26/02/09(月)15:06:01No.124626+2026gと11個の帰納的な関係式から |
| … | 93無題Nameベイズ厨 26/02/10(火)05:33:28No.124627+沙川熱力学面白いですね |
| … | 94無題Nameベイズ厨 26/02/10(火)05:45:52No.124628+ΔSはma=Fの加速度aに相当する |
| … | 95無題Nameベイズ厨 26/02/10(火)06:19:36No.124629+あとは静順過程で熱力学関数を時間の関数で表示して |
| … | 96無題Nameベイズ厨 26/02/10(火)06:36:28No.124630+ケプラーの法則や熱力学関数みたいな観測量と観測量の関係式は |
| … | 97無題Nameベイズ厨 26/02/10(火)08:51:25No.124631+物理屋からすると気体分子とエネルギー量子とエントロピー量子?から考えるミクロ的離散的なモデル(F 1/T S W)による統計力学がマクロ熱力学より汎用性があるように思えるが、 |
| … | 98無題Name名無し 26/02/10(火)22:44:16No.124633+ 1770731056444.jpg-(5962 B) 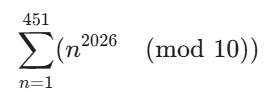 1から451までの整数をそれぞれ2026乗して1の位の数を求めます。 |
| … | 99無題Name名無し 26/02/13(金)23:43:02No.124640+>1から451までの整数をそれぞれ2026乗して1の位の数を求めます。 |
| … | 100無題Name名無し 26/02/14(土)01:20:03No.124641+mod 10 で考えると各数の2026乗の値は |
| … | 101無題Name名無し 26/02/14(土)23:29:15No.124649+ 1771079355057.jpg-(150156 B) 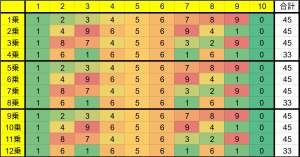 >mod 10 で考えると各数の2026乗の値は |
| … | 102無題Name名無し 26/02/15(日)19:37:51No.124663+ 1771151871831.jpg-(1091638 B)  >因みに Σ_{k=1}^{51} {n^2026 mod 100} も 2026 になる |
| … | 103無題Nameベイズ厨 26/02/16(月)07:15:34No.124665+>No.124611 |
| … | 104無題Nameベイズ厨 26/02/16(月)07:34:12No.124666+>No.124663 |
| … | 105無題Name名無し 26/02/16(月)13:39:14No.124672+>100と繰り返しのでる回数の関係式ってあるんでしょうか |
| … | 106無題Nameベイズ厨 26/02/17(火)08:28:52No.124676+ありがとうございます |
| … | 107無題Name名無し 26/02/17(火)20:29:32No.124679+ 1771327772390.jpg-(1769319 B)  >ありがとうございます |
| … | 108無題Name名無し 26/02/18(水)09:24:11No.124681+スレッドを立てた人によって削除されました |