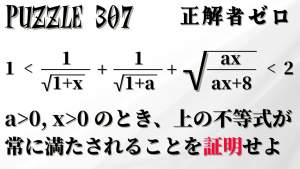 無題Name名無し25/12/13(土)18:52:09No.124194+
2月23日頃消えます
無題Name名無し25/12/13(土)18:52:09No.124194+
2月23日頃消えます
中国の入試で一番難しかった問題の一つらしい削除された記事が4件あります.見る
スマートな解き方はあるのか?
| … | 1なーNameなー 25/12/13(土)23:18:46No.124195そうだねx1なー |
| … | 2無題Name名無し 25/12/14(日)09:56:09No.124200そうだねx1エナブラおじさんの煽りは1行目と2行目が繋がってないのばかりで |
| … | 3無題Name名無し 25/12/14(日)09:57:08No.124201+α=1項目 |
| … | 4無題Name名無し 25/12/14(日)23:36:43No.124210そうだねx1a+x=p, ax=q とおくと問題は |
| … | 5無題Name名無し 25/12/15(月)15:38:21No.124223そうだねx2この問題は最大や最小がα=β=γの所にないので |
| … | 6なーNameなー 25/12/15(月)15:56:40No.124224+なー |
| … | 7無題Nameベイズ厨 25/12/26(金)07:07:34No.124295+エレガントな回答ないんでしょうか |
| … | 8無題Name名無し 25/12/26(金)11:42:15No.124296そうだねx3>0<α<1,0<β<1,0<γ<1 |
| … | 9なーNameなー 25/12/26(金)13:40:49No.124297+なー |
| … | 10なーNameなー 25/12/27(土)06:06:43No.124301+なー |
| … | 11無題Name名無し 26/01/03(土)17:29:44No.124402そうだねx1数学板には天才もいるからね。天才をもってしても解けないらしいね。 |
| … | 12無題Name名無し 26/01/04(日)11:32:42No.124408+不等式の証明に背理法使うことあるんだ |
| … | 13無題Name名無し 26/01/05(月)13:00:54No.124416+>>0<α<1,0<β<1,0<γ<1 |
| … | 14無題Name名無し 26/01/05(月)16:59:03No.124419+三項めの8が使えそうですね |
| … | 15無題Name名無し 26/01/09(金)14:10:18No.124444+簡単でしょ |
| … | 16無題Name名無し 26/01/09(金)15:33:17No.124445+もし整数と言う条件でないとしたら、問題は嘘である |
| … | 17無題Name名無し 26/01/09(金)15:53:06No.124446+ 1767941586261.png-(19884 B)  AIに問題の画像アップロードしたら |
| … | 18無題Nameベイズ厨 26/01/09(金)20:59:43No.124447+整数ではなくて独立という条件では? |
| … | 19無題Nameベイズ厨 26/01/22(木)11:25:11No.124514+3次方程式の解と係数の関係使えないでしょうか |
| … | 20無題Name名無し 26/01/22(木)20:45:11No.124519+設問が極めて異常で、「不等式」の前提にあり、不等なんだから決して満たされません。 |