 無題Name名無し24/12/31(火)08:32:53No.121452+
12月09日頃消えます
無題Name名無し24/12/31(火)08:32:53No.121452+
12月09日頃消えます
2025年にちなんで削除された記事が6件あります.見る
2025に関係ある問題スレ
| … | 1無題Name名無し 24/12/31(火)08:34:38No.121453+ 1735601678097.jpg-(74541 B) 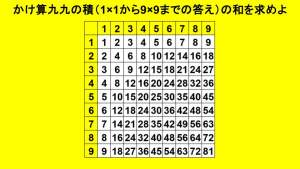 エクセル等で |
| … | 2無題Name名無し 24/12/31(火)09:50:14No.121454+>エクセル等で |
| … | 3無題Name名無し 24/12/31(火)15:23:29No.121455+ 1735626209261.jpg-(35806 B)  >系として自然数の3乗和の公式から |
| … | 4無題Name名無し 25/01/01(水)10:59:14No.121456+ 1735696754119.jpg-(60618 B)  力技で答えがでると思って作ってみたけど |
| … | 5無題Name名無し 25/01/01(水)15:39:32No.121457+ん? |
| … | 6無題Name名無し 25/01/01(水)17:57:02No.121458+>エクセル等で |
| … | 7無題Name名無し 25/01/01(水)18:42:52No.121459+ 1735724572740.jpg-(53860 B) 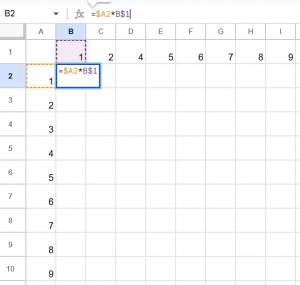 >ドラッグでずるっと簡単にやるにはどうすればいいんだ |
| … | 8無題Name名無し 25/01/02(木)06:51:17No.121460+>ん? |
| … | 9無題Name名無し 25/01/02(木)16:58:19No.121461+>A2のAを固定したいのでAの前に$つけて$A2 |
| … | 10無題Name名無し 25/01/03(金)06:20:51No.121463+ 1735852851915.jpg-(2698097 B)  >そうそう。後はコピーするセルを指定して、セルの右下にカーソル持っていって、表全体にドラッグして広げればOK |
| … | 11無題Name名無し 25/01/17(金)01:08:32No.121478+>このくらいなら簡単な大学入試レベルで出そう |
| … | 12無題Name名無し 25/01/18(土)14:49:12No.121479+0〜9までの整数が書かれたカードが1枚ずつ計10枚ある。(6と9は区別する) |
| … | 13無題Name名無し 25/01/18(土)23:52:50No.121480そうだねx1>このとき、積XYが2025になる確率は? |
| … | 14無題Name名無し 25/01/19(日)08:48:56No.121481+>積XYが2025になる確率は(1/45)^2=1/2025 |
| … | 15無題Name名無し 25/02/19(水)12:20:56No.121620+書き込みをした人によって削除されました |
| … | 16無題Name名無し 25/02/19(水)12:23:53No.121622+ 1739935433235.png-(7057 B) 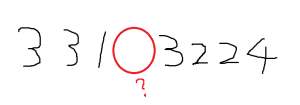 赤丸に入る数字は何でしょう |
| … | 17無題Name名無し 25/02/22(土)01:05:58No.121628+2025 |
| … | 18無題Name名無し 25/08/07(木)17:17:22No.122018+2^2025の桁数を求めよ |
| … | 19無題Name名無し 25/08/07(木)22:44:32No.122020そうだねx1>赤丸に入る数字は何でしょう |
| … | 20無題Name名無し 25/08/08(金)23:13:18No.122021+>赤丸に入る数字は何でしょう |
| … | 21無題Name名無し 25/08/09(土)01:50:18No.122022+>何でも入るだろ |
| … | 22無題Name名無し 25/08/09(土)04:19:52No.122023+>書いた本人も忘れていたけど正解は3でした |
| … | 23無題Name名無し 25/08/09(土)14:30:45No.122024+ 1754717445988.png-(16295 B)  >>赤丸に入る数字は何でしょう |
| … | 24無題Name名無し 25/08/09(土)17:10:59No.122025そうだねx1>に,せ,ん,に,じ,ゅ,う,ご の画数(接地回数)か |
| … | 25無題Name名無し 25/08/10(日)01:28:23No.122027+>その理由は? |
| … | 26無題Name名無し 25/08/10(日)11:59:03No.122029+書き込みをした人によって削除されました |
| … | 27無題Name名無し 25/08/10(日)12:00:00No.122030そうだねx1f(1)=3, f(2)=3, f(3)=3, f(4)=1, |
| … | 28無題Name名無し 25/08/10(日)17:56:19No.122035+>>赤丸に入る数字は何でしょう |
| … | 29無題Nameベイズ厨 25/08/11(月)05:20:10No.122038+クイズとしては面白いけど、数学としては好みの |
| … | 30無題Name名無し 25/08/11(月)17:13:25No.122040+>>何でも入るだろ |
| … | 31無題Name名無し 25/08/11(月)18:32:14No.122041+書き込みをした人によって削除されました |
| … | 32無題Nameベイズ厨 25/08/12(火)11:49:20No.122042+にせんにじゅうご |
| … | 33無題Nameベイズ厨 25/08/13(水)06:16:25No.122047+2025と331X3~ |
| … | 34無題Nameベイズ厨 25/08/17(日)13:23:25No.122055+2025のスレの文脈がなければ何でも入る |
| … | 35無題Name名無し 25/08/18(月)12:07:59No.122067そうだねx1問題を改定したらなんでも入るのは当たり前 |
| … | 36無題Name名無し 25/08/19(火)20:54:41No.122071+https://www.youtube.com/watch?v=mwwH_AJWUMI |
| … | 37無題Name名無し 25/09/05(金)03:02:39No.122154+10,20,40,80,160,320 の6つの数字を使って以下のルールで2025を導き出してください |
| … | 38無題Name名無し 25/09/05(金)03:24:54No.122155+例) 10,20,30,40,50,60の6つの数字を使って2025を導き出す |
| … | 39無題Name名無し 25/09/07(日)05:23:05No.122163+書き込みをした人によって削除されました |
| … | 40無題Name名無し 25/09/07(日)06:40:33No.122164+書き込みをした人によって削除されました |
| … | 41無題Name名無し 25/09/07(日)06:41:20No.122165+>問題を改定したらなんでも入るのは当たり前 |
| … | 42無題Nameベイズ厨 25/09/07(日)07:32:03No.122166+どうやって逆問題解いたんでしょうか |
| … | 43無題Name名無し 25/09/07(日)08:10:21No.122167+>10,20,40,80,160,320 の6つの数字を使って以下のルールで2025を導き出してください |
| … | 44無題Name名無し 25/09/07(日)08:43:28No.122168+>>810×400=32400 |
| … | 45無題Name名無し 25/09/07(日)13:03:52No.122169そうだねx1>No.122167 |
| … | 46無題Name名無し 25/09/07(日)13:07:27No.122170そうだねx1>どうやって逆問題解いたんでしょうか |
| … | 47無題Name名無し 25/09/07(日)22:54:14No.122171+>No.122170 |
| … | 48無題Nameベイズ厨 25/09/08(月)05:42:05No.122193+線形代数そう使えるんですね |
| … | 49無題Name名無し 25/09/15(月)16:46:02No.122201+スレッドを立てた人によって削除されました |